Contractual equations
Algebra for double-entry accounting
Prof. Elham Saeidinezhad's new working paper builds out a Money View of FX swaps. Readers of Soon Parted will find in Dr. Saeidinezhad's paper a familiar set of conceptual reference points—attention to accounting, a hierarchical monetary system, market-making. The paper also develops the deep connection between FX swaps and repo as money-market instruments, which sheds light on the structure of the global dollar, including the Fed's role as international lender of last resort.
Though it is not the core of the paper, I was struck by Dr. Saeidinezhad's use of contractual equations to make sense of complex financial instruments. This way of understanding financial instruments—an algebra of double-entry accounting—fits nicely with other balance-sheet approaches. In this post, I translate Elham's contractual equation example into my own terms.
Algebra with cash flows
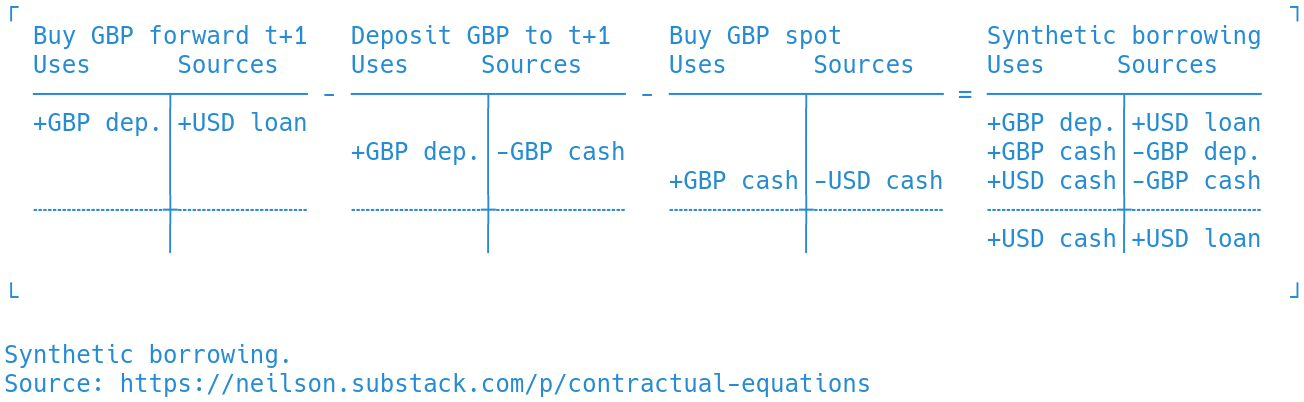
The example deals not with FX swaps but with FX forwards—an agreement to exchange cash in one currency for cash in another, at an agreed future date, according to terms agreed today. These T accounts show one way to think of an FX forward as a combination of other instruments. They use sources and uses accounting, and are written from the point of view of a buyer of forward British pounds. From left to right, the buyer obtains dollars through a loan, sells them for GBP in a spot FX transaction, and deposits the pounds. Only the creation of the forward is shown: at maturity, the deposit will mature, yielding cash in GBP, and the loan will mature, absorbing cash in USD, the same as a forward FX transaction.
The transactions are written as an equation,
USD loan + Spot FX + GBP deposit = FX forward. On the right-hand side, flows of both USD cash and GBP cash net out, leaving only the forward flows, shown below the dotted line. The FX forward, in other words, achieves in a single instrument the same net cash flows as the three transactions on the left. If it were expanded to show quantities for each entry, this contractual equation would be a statement of the covered interest parity (CIP) no-arbitrage condition.
By thinking of the T accounts as components of an algebraic expression, we are invited to use familiar algebraic steps to rearrange the terms, and it turns out that such operations are meaningful. For example, rearranging the above we can write
FX forward - GBP deposit - Spot FX = Loan. This expression can be translated back into T accounts. As Prof. Saeidinezhad notes, when the entries are written with a minus sign, it means that the transactor is taking the opposite side of the transaction, so on the right-hand side, increases become decreases and vice versa, and uses become sources and vice versa.
This becomes a bit easier to read if we re-write it with plus signs instead of minus signs. The third set of T accounts below say exactly the same thing as the second set.
Economically, this says that one can create the cash flows of a loan of dollars by buying GBP forward, accepting a GBP deposit, and using the proceeds to purchase USD now. One could then think about the financial engineering questions that this raises (how can this synthetic loan be created from available instruments?), or about market-making questions (do markets for these instruments exist, and are they liquid?).
A helpful tool for balance-sheet thinking
But for now, I just want to highlight the technique, and Prof. Saeidinezhad's paper for taking the time to explain it. This way of manipulating cash-flow accounting seems like a useful addition to the balance-sheet reasoning toolkit. It says that an algebraic logic applies to sources and uses ledgers, so they can be transformed like equations. The responsibility to ensure that the resulting arguments are good ones, of course, remains with the thinker.



Isn't the paper saying Covered Interest Parity is violated because dealers deserve riskless arbitrage profits?
《At the same time, the literature documents that most active investors have not been able to outperform passive investment strategies.
Treynor offers his insights on these matters in a series of articles. In general, the portfolio managers’ actual returns fail to exceed market averages. The failure is due to the dealer-based quality of the capital market and the presence of the dealers’ spreads.》
《 [...] as the dealers expand their balance sheets, they demand higher premiums from their clients to provide synthetic dollar funding (e.g., borrowing in euros and swapping into
dollars) relative to direct dollar funding (i.e., borrowing dollars in the money market), resulting in CIP deviations. They earn an extra premium by increasing the forward rates compared to spot rates: As F/S
increases, the relative cost of purchasing the US-Dollar at maturity compared to the spot contract falls. As the dealers are the sellers of dollars in the spot and the buyers of them in
forward, the dealer can obtain more units of dollars with the same amount of foreign currency as the forward rate increases relative to the spot rate.》
In other words, do dealers profit from riskless arbitrage, backstopped in case of counterparty default by the Fed?
What are the implications of the violation of no-arbitrage conditions on fair pricing models? Do prices become arbitrary?